
Thus a graph of position versus time gives a general relationship among displacement(change in position), velocity, and time, as well as giving detailed numerical information about a specific situation. Using the relationship between dependent and independent variables, we see that the slope in the graph above is average velocity and the intercept is position at time zero-that is, Substituting these symbols into gives Shows a graph of position versus time for a jet-powered car on a very flat dry lake bed in Nevada.įigure 2.47 Graph of position versus time for a jet-powered car on the Bonneville Salt Flats. Figure 2.47 is just such a straight-line graph. A graph of position versus time would, thus, have on the vertical axis and t on the horizontal axis. Time is usually an independent variable that other quantities, such as position, depend upon.

The letter is used for the -intercept, which is the point at which the line crosses the vertical axis.įigure 2.46 A straight-line graph. Here is the slope, defined to be the rise divided by the run (as seen in the figure) of the straight line. If we call the horizontal axis the -axis and the vertical axis the -axis, as in Figure 2.46, a straight-line graph has the general form

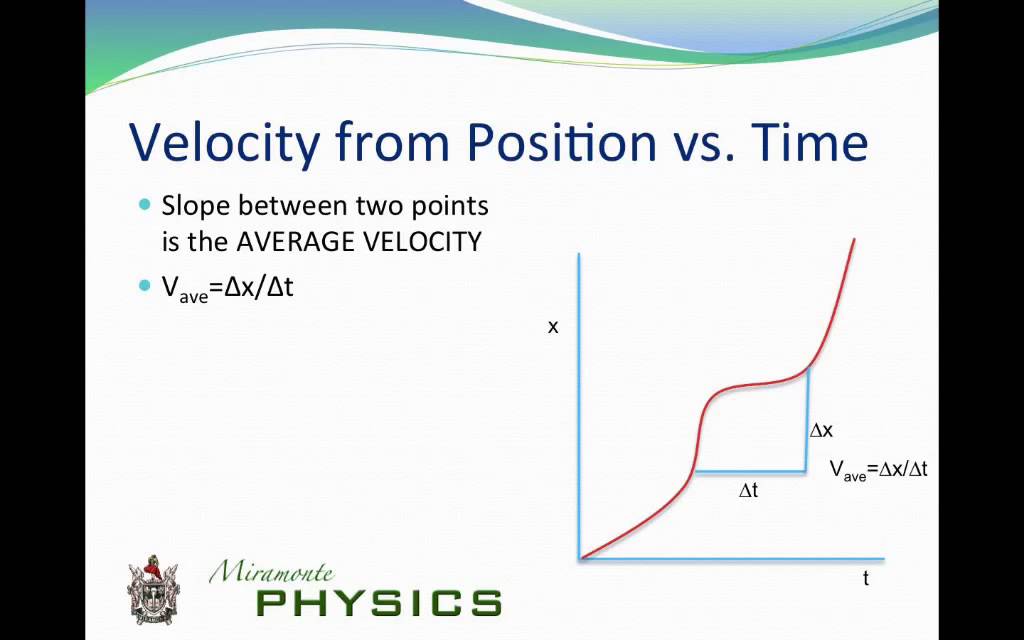
When two physical quantities are plotted against one another in such a graph, the horizontal axis is usually considered to be an independent variable and the vertical axis a dependent variable. This section uses graphs of position, velocity, and acceleration versus time to illustrate one-dimensionalįirst note that graphs in this text have perpendicular axes, one horizontal and the other vertical. Graphs not only contain numerical information they also reveal relationships between physical quantities. Therefore, the slope of the velocity versus time graph is acceleration.Ī graph, like a picture, is worth a thousand words. The slope of this linear graph has units, which are acceleration units. This process is demonstrated in Figure 2.48 (a) and (b). Then, we can use that table to plot velocity versus time. We can determine instantaneous velocities at multiple points along a position-time graph with constant non-zero acceleration and make a table relating these instantaneous velocities to the specified time along the x-axis where we found them. When analyzing motion, graphs representing values of various parameters of motion make it simpler to solve problems. To determine instantaneous velocity at a given time when acceleration is a non-zero constant, take a look at Example 2.18. Graphical Representation makes it simpler for us to understand data. Pay attention to the tangent lines drawn in Figure 2.48 (a). The instantaneous slope can be determined by drawing a tangent line at the desired point along the graph and determining slope. Consider an object that moves with a constant velocity of +5 m/s for a time period of 5 seconds and then accelerates to a. In the position versus time graph, the slope at any given point is the instantaneous velocity of the object. Note that while the position versus time graph is not linear, the velocity versus time graph is linear. You can see an example of this type of graph in Figure 2.48. When acceleration is a non-zero constant, the graph of position versus time is no longer linear.
PHYSICS GRAPHICAL ANALYSIS HOW TO
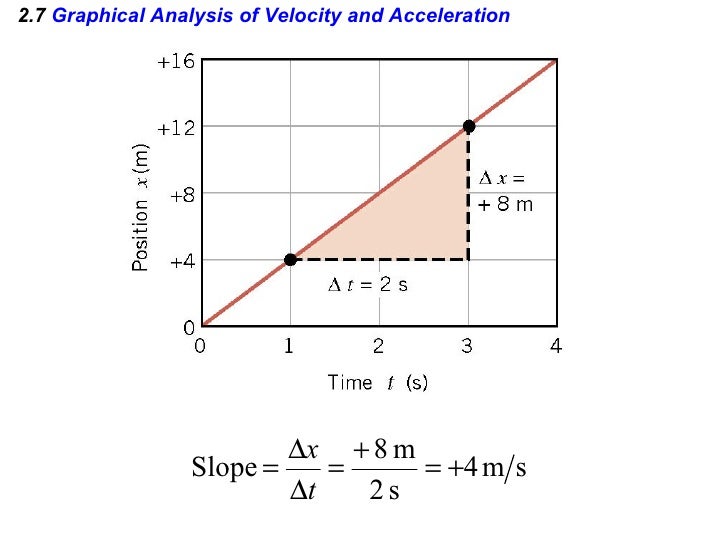
See how to calculate the average velocity of an object from this type of graph in Example 2.17. Therefore, the slope for a graph of position versus time with zero acceleration is the average velocity of that object. In this case, the unit for slope is m/s, which is the unit for velocity. In this graph, we can determine the slope by picking two different points on the line, taking the change in y-value, and dividing it by the change in x-value between those two points. See an example of this type of graph in Figure 2.47. As you read, pay attention to Figure 2.46 which is an example of a linear graph is the graph of position versus time when acceleration is zero. (c) Acceleration gradually declines to zero when velocity becomes constant.Read this text for an introduction on graphical position, velocity, and acceleration with regards to one another. The slope of this graph is acceleration it is plotted in the final graph. (b) The velocity gradually approaches its top value. (a) The slope of this graph is velocity it is plotted in the next graph.
This motion begins where the motion in ends. Graphs of motion of a jet-powered car as it reaches its top velocity.
Similarly, velocity increases until 55 s and then becomes constant, since acceleration decreases to zero at 55 s and remains zero afterward. Graphs of Motion when a size 12, after which time the slope is constant.


 0 kommentar(er)
0 kommentar(er)
